New move representation

See Mediocre v0.22b

It is time to start looking at ways to improve the general performance of Mediocre.

All the changes I will be doing for the next version will be fixing general performance issues. Basically Mediocre will return the exact same moves for a certain ply, only that it (hopefully) will reach the ply much faster.

Here are a few things I will be looking at.

Vectors

I have been using the Vector-class (located in the Java library) for storing moves in different forms. While the Vector-class is very easy to use, it is also slow. Much slower than using an array.

I will be changing the code wherever I have used Vector and use an array instead. This will make the code a bit more awkward, but speed it up a notch or two.

A new move representation

This is where I think the main speed gains can be found. Up until now I have used the Move-class to create objects representing moves. Since Java is an object-oriented language this is the preferred way for simplicity and good encapsulated code (it is not like I encapsulate anything anyway :) ).

But a chess program needs speed more than good looking code, and creating an object takes time.

I was actually warned about this in a comment back in december when I started writing Mediocre, but I think I chose the right path. First create a working program that is easy to understand, and then (now) start making optimizations to the working code.

I plan to represent the moves with an integer. An integer has 32 bits (ones and zeros) and I will use different bits to represent different things about the move.

To represent a square on the 0x88 board we need 7 bits since that can hold number between 0 and 127. So the 'to' and 'from' indexes needs 7 bits each.

To represent a piece we need 4 bits, which can hold a number between 0 and 15. (6 white and 6 black pieces + empty square = 13 so it is enough) This will be used to hold what piece is moving and what piece is captured.

We also need 3 bits for the movetype. 3 bits can hold a number between 0 and 7, and that is exactly the number of move types we have (ordinary, en passant, long and short castling, promotion to queen, rook, knight and bishop).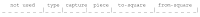

So we need; 7+7+4+4+3 = 25 bits which fits in the integer's 32 bits. Which I illustrate in the image.

Storing valuesin the int

To store values we use the shift << and or | operators. This is done like this:

int toShift = 7;
int pieceShift = 14;
int captureShift = 18;
int typeShift = 22;

int move = -1;

move =
(from)
| (to << toShift)
| (piece << pieceShift)
| (capture << captureShift)
| (type << typeShift);

We 'shift' the values to the right position and then use 'or' which changes the right bits to 1 instead of 0. It could look like this:

Let us say we want to add to=54 to our 32-bit integer.

54 = 110110 (in binary from)

And we have a long row of zeros we want to add it to.

...0000000000000000000000000

Now we shift the 54 to the right position. That is we add seven zeros behind it like this:

1101100000000

And now we 'or' it to the row of zeros:

...0000000000000000000000000
OR ...0000000000001101100000000
= ...0000000000001101100000000

If we want to add type=5 (101). Shift it to the right position (i.e. add 22 zeros behind it):

1010000000000000000000000

And then 'or' it to the integer:

...0000000000001101100000000
OR ...1010000000000000000000000
= ...1010000000001101100000000

So now we have the type in the right position and so on for all the other values. The 'from'-position is in the beginning so we do not need to shift it.

Retrieving values from the int

Now we have a long row of 1's and 0's. In decimal form it looks cryptic (a high random number like 9698192 or so), but we do not need to worry about that.

To retrieve a value we do like this:

int squareMask = 127;
int pieceMask = 15;
int typeMask = 7;

from = (move & squareMask);
to = ((move >> toShift) & squareMask);
piece =((move >> pieceShift) & pieceMask);
capture = ((move >> captureShift) & pieceMask));
type = ((move >> typeShift) & pieceMask));

First we shift the piece of the code we want to the beginning. Then we apply a 'mask' and 'and' with it, it could look like this like this to retrieve the to-value:

...10010110110001101011001011
Shift:
...00000001001011011000110101 (the to-values are now first)

And with the mask:

...00000001001011011000110101
AND ...00000000000000000001111111
= ...00000000000000000000110101

We now have the to-value.

It is worth it

This system can be very cryptic at first, and it is easy to get wrong. But on the other hand bitwise operations are extremely fast since the computer is working directly with the bits and do not have to convert them first.

Since we replace the Move-objects with a very fast scheme, the gains should be very good.

The time difference in creating the different types of moves is huge, the scheme I have now explained is almost 20 times faster than using an object.

And that does not include every little time gain we will get from not having to access the values through an object, but instead doing an extremely fast bitwise operation.

The 'downside'

Until now Mediocre has handled unmaking moves through the Move-object itself. The move stored information about the previous position and made unmaking possible.

Unfortunately we can not fit that information in a 32 bit integer, it would require about 49 bits total, slightly less with some optimization.

To fit that information we would have to use the type 'long' which has 64 bits. But firstly, handling the long type is much slower than handling integers, and secondly 64 bits takes twice as much memory which will become important when we start looking at optimizing and resizing the transposition table.

So we will have to find another way to store information about passed positions. There is an easy way to do this which I will explain later.

We have 7 bits to spare

As I showed above it takes 25 bits to represent a move, so we have 7 unused bits. I am thinking about using them to store the ordering value. 7 bits can represent a value between 0 and 127 so it should be enough, but I would have to tweak the move ordering values slightly to fit them (especially from killer moves and the history heuristic).

Work that does not change the engine

I will start making these changes right away. Large parts of the code has to be rewritten, especially the make and unmake-move methods, and also the move generation. I hope to make them more efficient as well.

Hopefully this will speed up Mediocre by a great deal.